Operaciones con matrices

Suma de matrices

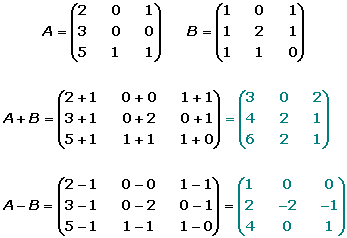
Dadas dos matrices de la misma dimensión, A=(a_ij) y B=(b_ij), se define la matriz suma como: A+B=(a_ij+b_ij).

La matriz suma se obtienen sumando los elementos de las dos matrices que ocupan la misma misma posición.

Propiedades de la suma de matrices

Interna:

La suma de dos matrices de orden m x n es otra matriz dimensión m x n.

Asociativa:

A + (B + C) = (A + B) + C

Elemento neutro:

A + 0 = A

Donde O es la matriz nula de la misma dimensión que la matriz A.

Elemento opuesto:

A + (−A) = O

La matriz opuesta es aquella en que todos los elementos están cambiados de signo.

Conmutativa:

A + B = B + A

Producto de un escalar por una matriz

Dada una matriz A=(a_ij) y un número real kR, se define el producto de un número real por una matriz: a la matriz del mismo orden que A, en la que cada elemento está multiplicado por k.

kA=(k a_ij)

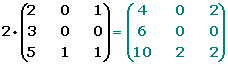
Propiedades

a ·  (b · A) = (a · b) · A A  M_mxn, a, b 

a  ·  (A + B) = a · A + a · BA,B  M_mxn , a  

(a + b) · A = a · A + b · A A  M_mxn , a, b  

1 · A = A A  M_mxn

Producto de matrices

Dos matrices A y B son multiplicables si el número de columnas de A coincide con el número de filas de B.

M_{m x n} x M_{n x p} = M _{m x p}

El elemento c_ij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos.

Propiedades del producto de matrices

Asociativa:

A · (B · C) = (A · B) · C

Elemento neutro:

A · I = A

Donde I es la matriz identidad del mismo orden que la matriz A.

No es Conmutativa:

A · B ≠ B · A

Distributiva del producto respecto de la suma:

A · (B + C) = A · B + A · C